说到编译原理,是计算机科学里面很重要的一个学科,你可以说编译原理无处不在。但是一般人很少可以接触到这样的理论。编译原理分前端和后端,前端包括文本解析和类型检查,后端包括优化和代码生成等等。这篇日志里我主要讨论文本解析中一个最为简单的部分:数学表达式。
数学表达式: 1 + 1 * 3 * 3 + 4 / 4 * 5
要求出这个表达式的值,不禁让我想起了当时学习数据结构时候的习题,这样的表达式用栈来解决。
我们先要列出一个表,包括各种算术符的优先级
| 符号 | 优先级 |
|---|---|
| + | 1 |
| - | 1 |
| * | 2 |
| / | 2 |
然后我们需要两个栈,一个操作符的栈名为OP_STACK 一个数字的栈,名为NUM_STACK
因为我们的操作符都是耳目操作符,就是操作符左右都为值,比如说 1 * 1里面 1* 或者 *1 都是没有意义的,所以我们是一个数字,一个符号这样间隔读入的,这样就好办了:
- 把第一个数字入
NUM_STACK - 这时,读入(SHIFT)的是一个操作符,如果
OP_STACK顶为空,则入栈OP_STACK,如果不为空,则和OP_STACK栈顶比较,如果比OP_STACK栈顶优先级高,则入栈OP_STACK,否则的执行REDUCE操作,OP_STACK栈顶操作符出栈,NUM_STACK出栈两个数字,然后运算结果,再将结果入栈NUM_STACK,循环操作
操作流程如下:
| 表达式 | NUM_STACK |
OP_STACK |
对比结果 | 对应的操作 |
|---|---|---|---|---|
1+1*3*3+4 |
NUL | NUL | SHIFT | |
*3*3+4/4*5 |
1 1 | + | > | SHIFT |
*3+4/4*5 |
1 1 3 | + * | = | REDUCE |
*3+4/4*5 |
1 3 | + | > | SHIFT |
+4/4*5 |
1 3 3 | + * | = | REDUCE |
+4/4*5 |
1 9 | + | = | REDUCE |
+4/4*5 |
10 | NUL | SHIFT | |
/4*5 |
10 4 | + | > | SHIFT |
*5 |
10 4 4 | + / | >= | REDUCE |
*5 |
10 1 | + | > | SHIFT |
| NUL | 10 1 5 | + * | REDUCE | |
| NUL | 10 5 | + | REDUCE | |
| NUL | 15 | NUL |
这样马上我们就算出结果了,然而编译有时并不要求我们马上算出结果,有时只需要我们保存解析的结果,以便以后运行,或者生成代码等等操作,请看下面的表达式:
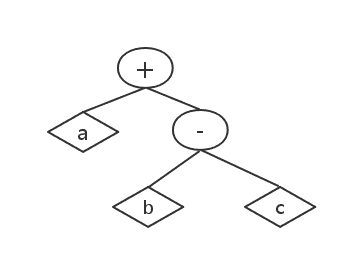
a + b * c
显然我们没办法马上算出结果,但是我们可以把它变成一棵树
显然这样就容易多了,这就是我们要说的解析(parsing),如何解析呢?方法其实和上面是一样的,不过要做一点点改动,我们知道乘法优先级比较高,当我们计算b * c的时候,我们并不是真的相乘,我们只是创建一个新的结点,把b和c作为子节点,然后把这个新结点入栈,就可以了。
有了这科语法树之后,当我们知道a b c的值之后,就可以递归算出结果了,我们要计算根节点的结果,就要首先计算子节点的结果,最后回溯可得答案。当然,从另一方面,你可以通过这棵树生成中间代码,或者机器码,这样就编译出真正的程序了。